
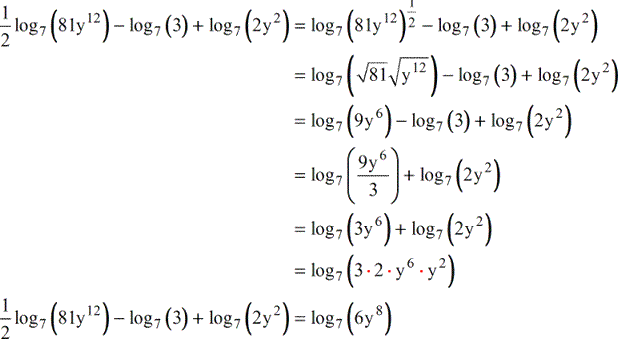
It allows you to take the exponent in a logarithmic expression and bring it to the front as a coefficient. This property will be very useful in solving equations and application problems. Two log expressions that are subtracted can be combined into a single log expression using division. This property allows you to take a logarithmic expression involving two things that are divided, then you can separate those into two distinct expressions that are subtracted. Two log expressions that are added can be combined into a single log expression using multiplication.

This property allows you to take a logarithmic expression of two things that are multiplied, then you can separate those into two distinct expressions that are added together. This property says that if the base and the number you are taking the logarithm of are the same, then your answer will always be 1.

You can verify this by changing to an exponential form and getting. This property says that no matter what the base is, if you are taking the logarithm of 1, then the answer will always be 0. You can verify why this works by changing to an exponential form and getting and anything to the zero power is 1.

In addition to the property that allows you to go back and forth between logarithms and exponents, there are other properties that allow you work with logarithmic expressions. This problem is nice because you can check it on your calculator to make sure your exponential equation is correct. In the logarithmic form, the 625 will be by itself and the 4 will be attached to the 5. The 625 was attached to the 5 and the 4 was by itself. Since the base is the same whether we are dealing with an exponential or a logarithm, the base for this problem will be 5. So when we switch those values, the 2 is by itself and the 8 is “attached” In this case the 2 is “attached” to the 3 and the 8 is by itself. It doesn’t matter if x and y are variables or numbers. In the exponential form in this problem, the base is 2, so it will become the base in our logarithmic form.īecause logarithms and exponents are inverses of each other, the x and y values change places. When changing between logarithmic and exponential forms, the base is always the same. Change the exponential equation to logarithmic form.is exactly the same as You can use the above property to change a logarithmic expression into an exponential expression or an exponential expression into a logarithmic expression. This leads to the most basic property involving logarithms which allows you to move back and forth between logarithmic and exponential forms of an expression. You may recall that when two functions are inverses of each other, the x and y coordinates are swapped. Here is a video with a similar example worked out.Logarithmic functions and exponential functions are connected to one another in that they are inverses of each other. Since these base of the exponential expressions are the same, combine using the power and quotient rules for exponent.įind a common denominator to combine the fractions. Product Rule for Logarithms: Quotient Rule for Logarithms: The expressions inside the logarithm will be positioned in the numerator if the logarithm is positive or will be positioned in the denominator if the logarithm is negative. A fourth root is the same as the one-fourth powerĬondense the logarithms using the product and quotient rule. A square root is the same as the one-half power. The coefficient of 1/6 on the middle term becomes the power on the expression inside the logarithmĪ radical can be written as a fractional power. Whenever possible, evaluate logarithmic expressions. Problem: Use the properties of logarithms to rewrite the expression as a single logarithm.


 0 kommentar(er)
0 kommentar(er)
